Children's Error in “Addition
Yam Prasad Pandeya
Siddhajyoti Education Campus
Abstract
It is based on a
study concerned errors made by children of primary school while performing an
addition operation. The addition is one of the basic mathematical operations
that children practices in early classes. This research was intended to find
out the types of an error made by children in addition. The researcher prepared a questionnaire containing
20 different questions focusing on children of 5 to 7 years. Five schools were
selected by purposive sampling and 50 students by random sampling. A test was
administered among them and analyzed the errors made by them. The findings
revealed that many children had confusion about the basic fact of “Addition” as
they made mistakes while setting numerals as horizontally and, some children
wrote the carried number in answer, some of them forgot carried number, and
some added the carried number twice and some children made errors by starting
to add from the left-hand side.
Keywords: Children, Addition,
Error, Early class
Introduction
Mathematics
as a subject in the school curriculum is compulsory, both at the Primary and
High schools. It also plays leading and important roles in all aspects
of human endeavor. The use of mathematics is found in many areas of real-life
situations. The field of management, business, and marketing is no
exception. In the history of education, mathematics has held its leading
position among all other school subjects because it has been considered an
indispensable tool in this technological fast-growing world.
The foundation blocks of mathematics are made
up of the concepts of additions and subtractions. Therefore no building of
mathematics can be put up without the solid basic foundation concept,
which is, addition. It is one of the most important concepts of mathematics
and one inability to do simple addition, fails to climb the academic
ladder of education to its topmost height
The addition is one of the basic
mathematical concepts that children learn. “Addition” is considered a crucial
skill because it is the most basic elementary concept that has a vital effect
on the development of several other concepts related to mathematics, such as
problem-solving, computation, subtraction, etc. level. According to Kim, addition
is the mathematical process of putting the thing together. The plus sign “+”
means that two numbers are added together.
The concept of addition, according to the Oxford
Learner’s Advance Dictionary (2001), “is the process of adding two or more
numbers of distinct values together to find their totals”. Atuahene
(2019, p. 8), says, " addition refers
to the act of putting two or more things together to increase the size, number,
amount and so on. Addition and subtraction are the basis of
mathematics". The
main idea which is mostly used in our daily activities brings to light that
almost all the concepts in mathematics are developed out of addition. For instance, the concept of measurement and algebra are made up
of addition.
From Land (1975), the letter and symbols which denote numbers are the short forms of mathematics and for that matter, greater attention should be given to it to make pupils understanding permanent to foster learning in the classroom. More so, it has been noted that most pupils normally find it very uneasy to cope with addition involving the place value concept.
Children
learn this concept both formally and informally through interaction with others
in their surroundings. But students make errors while learning it. Some researches
undertaken by educationists tried to identify errors made by pupils. ( as cited
in Munasinghe,p.1)
According to Collins (1982) Dictionary, "an ‘error’ is something we have done which is considered to be incorrect or wrong". Ernest (1996, p.802) says, Many people’s images of mathematics represent mathematics negatively, such that mathematics is perceived to be "difficult, cold, abstract, and in many cultures, largely masculine". This is because most students make mistakes in understanding mathematical concepts during the early stage of learning, and this affects their ability in mathematics at a higher level. This is because most students make mistakes in understanding mathematical concepts during the early stage of learning, and this affects their ability in mathematics at a higher level.
Literature
has shown many classifications of pupil errors in which they are grouped
according to different criteria; groups such as systematic errors, random
errors careless errors which are found to be common. Random errors and Careless
errors are found to be common. Systemic errors are those that occur due to a lack
of understanding or incorrect understanding of concepts and principles. Random
errors show no discernible relationship to the problems. Careless errors may be
accidental.
Munasinghe
(2013, p.5 ) says, “
Teaching instruction procedure has to be designed to reduce the problems
encountered by the primary school children with “addition” of numbers. Further,
the teacher has to pay individual attention to children and s/he should provide
practice sessions to children on the representation of numerals. Further, the
study points to the parental and teacher caring when guiding basic mathematical
and linguistic skills by using the correct language with children preparing
necessary environmental factors”.
There are
very few researchers' findings that show that most primary school children face
mistakes of addition at primary school. Primary school children have to be able
to read numbers like 1…2…3…4… from memory. This is the rote or mechanical
learning process where they are not aware of the fact that these numbers are
arranged in a certain order or that each number has a definite position on the
number sequence. Children are required to develop the ability to perform the
“addition” of three numerals carry over is involved. Somehow the main aim of
the research was to identify error patterns in addition made by grade two (5 to7years)
children in performing “addition” involving 2 or 3 digits with carrying out.
Most of the students consider mathematics a difficult subject. The primary level students make many errors in performing addition operations. This is because they cannot understand all the rules of addition and when we teach different rules they forget the previous rule which they already learned. If students cannot perform addition operations properly then it will be very difficult to teach them other methods like subtraction, multiplication, and division. So, they should have a clear concept about “Addition”. This research tried to find the errors made by primary-level students.
The Study
A study
on assessment of pupils' achievement in primary mathematics with special
reference to the analysis of errors diagnosed through interviews was carried
out by (Nanayakara, 2002) who tried to contribute towards the quality
improvement of mathematics education in Sri- Lanka. The study focused on
assessing pupil’s achievements in primary mathematics with emphatics on the
error patterns and underlying causes for the unusual achievement patterns. The
study focused on systemic errors which occur due to a lack of understanding of
concepts. Conceptual error patterns regarding the concept of addition were
identified in the research. They were;
·
Recalls
“Addition” basic facts incorrectly.
·
Starts
“Addition” from the left.
·
Totals
incorrectly when “0” is one of the numbers to be added.
·
Commits
errors due to lack of understanding of place value concept and carrying over the
concept.
Methodology
The
research design of this study was an experimental research design of quantitative search. Bhat(2019), said that "Experimental research is
any research conducted with a scientific approach, where a set of variables are
kept constant while the other set of variables are being measured as the
subject of experiment". In this, the researcher wished to find the types
of errors while children perform addition at the primary level. Hopkins
(2008. the quantitative research aim is to determine the relationship between
one thing (an independent variable) and another (a dependent or outcome
variable) in a population. Quantitative research designs are either descriptive
or experimental. The location of
the study was Kamalamai Municipality of Sindhuli district. The researcher had
selected five primary schools for data collection purposively. Ten students of 5 to 7 years were selected
using random sampling to administer the questionnaire. The researcher had employed
a questionnaire that consisted of 20 items of questions as a tool for data
collection. The researcher selected 50 students from 5 schools selecting 10
students from each school. The variables like age, sex socio-economic
background, educational achievement, and teachers’ responses have not taken
into account while selecting students
The entire information gathered from the primary sources was processed, analyzed, and interpreted. The descriptive method was used for analysis and interpretation of data presenting in tables and diagrams to show the result. The analysis of data was carried out through the coding process. The codes were categorical and thematic. The information of analyzed data was viewed from different theoretical perspectives. The collective data were encoded and similar information was kept in one basket. Firstly, the researcher collected the answer sheets and checked them to find how many children gave the right answer for all questions. At the same time, I find out how many questions were wrong there. After finding wrong answers, the researcher analyzed them to find out what sort of errors were committed. Finally, enlisted the different types of errors found in the answer sheets.
Analysis
and Interpretation
To collect the
data researcher had employed a questionnaire that consisted of 20 items of questions.
At the first stage of analysis of data the researcher separate the wrong and
right answer from all questions. After finding wrong answers, the researcher
analyzed them to find out what sort of errors were committed.
Students' performance
The percentage of students who gave write or wrong answers has been presented in the following table:

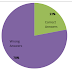
The
above pie-chart shows that very less number of children was able to give the
right answer and almost all children made any kind of mistakes. Among 50
students only 22% children gave the right answers and the remaining 78%
children made any type of mistake.
Number of
Incorrect Answers Given by Children
The
number of incorrect answers given by children has been presented in the
following table:
Table 1.
Numbers of Incorrect Answers
|
No. of questions |
No. of children |
Percentage |
|
1-5 |
2 |
5.12 % |
|
6-10 |
11 |
28.20 % |
|
11-15 |
14 |
35.89 % |
|
16-20 |
12 |
30.76 % |
From the
above table, we see that 2 children made 1 to 5 wrong answers and those who
made 6 to 10 incorrect answers were 11. Similarly, 14 did wrong for 11 to15 questions
and 12 children gave the wrong answer for 16 to 20 questions. Percentages of
students who made the different number of wrong answers have been given in the
above table.
Types of Errors Made by Children
Types of the error
made by children have been presented in the following table:
Table 2. Types
of error
|
S.N. |
Types
of error |
Nov
. of children |
|
1 |
Basic
fact error |
28 |
|
2 |
Added
carried number last |
3 |
|
3 |
Forgot
to add carried number |
7 |
|
4 |
Faulty
set down |
10 |
|
5 |
Added
from left to right |
8 |
|
6 |
Confused
with zero used in addition |
4 |
|
7 |
Carried
wrong number |
2 |
The above
table, shows that the students performed different errors, out of 50 children,
28 children made basic fact error, 3 children added carried number, at last,
forget to add the carried number by 7students, added from left to right by 8
students. The 4 students got confused to add zero and 2 students carried a
wrong digit.
Findings
The primary
school children made different kinds of errors. Some children have done some
random errors but most of the children revealed different kinds of error patterns.
Many children have confused about the basic fact of “Addition”. They made
mistakes while setting numerals horizontally. Even they didn’t know the number
in the unit’s place and add the number in unit place with the number in ten’s place.
Some children were found to be confused in addition to zero. Similarly, some
children wrote the carried number in answer, some of them forgot carried
number, and some added the carried number twice and some children made errors by
starting to add from the left-hand side.
Conclusion
Many
children have done some common errors and which can be eliminated by practice
and proper guidance. The teaching instruction procedure should be designed to address
the problems encountered by the primary school children with the addition of
numbers. The teacher has to pay individual attention to children and use
children centered teaching-learning process. While teaching, the teacher should
show the different types of errors made by children when performing addition.
Implications
This
study can be a reference material for primary-level mathematics education. This
study is also helpful for the course designers, book writers, publishers,
teachers, parents, and students. Specifically, the teacher can use the results
of this study while teaching in the classroom.
References
References
Atuahene E. (2019), Addition of Two and
Three-Digit Numbers In Primary Two, https://independent.academia.edu/EmmanuelAtuahene
Bhat
A.(2019), Experimental Research – Definition, https://www.questionpro.com/blog/experimental-research/
Collins (1982), COBUILD Advanced English Dictionary. HarperCollins Publishers.
Ernest, P. (1996). Popularization: myths, mass media, and
modernism. In A. J. Bishop
(Ed.), The International Handbook of Mathematics Education.Dordrecht:
Kluwer Academic.
Land Frank (1975), The Language of Mathematics, Britain, Murray John Publishers
Ltd
Hopkins W. G. (2008), Sportscience 4(1), sportsci.org/jour/0001/wghdesign.html,Department
of Physiology and School of Physical Education, University of Otago, Dunedin,
New Zealand 9001.
Land Frank (1975), The Language of Mathematics, Britain, Murray John Publishers
Ltd
Mottershead Lorraine (1985), Sources of Mathematics Discovery, Britain, Basil Blackwel, Oxford
Munasinghe D. M.
W. (2013), A study on error patterns in “Addition” in primary
schoolchildren (7 years old children), Merit
Research Journal of Education and Review,1(7)
Nanayakkar GSL
(2000), Assessment of pupil achievement in primary mathematics Sri- Lanka











No comments:
Post a Comment
If you have any doubts, please comment me